Skip to main content

Microstudies: Part 3

Is 🎶 workin' 9-to-5 🎶 a way to get a degree?

· 16 min read
James Finnie-Ansley

Dolly Parton's hit track "9 to 5" laments the woes of workin' 9 to 5 while barely gettin' by. Despite this treatise against work and the plight of the white-collar worker, many people still believe that in the case of youths, a job will "do them some good".

In a way, I agree — I worked in a café during my teenage years and feel my experience working in hospitality has made me vaguely more well-rounded. At least, I noticed this when I moved to student halls for my university study and had to interact with people who had, in their 18 years, never had to work a day in their life. However, working might be less of a fun personality-building exercise when it becomes less of a fun side-job and instead becomes a necessity — particularly if work might get in the way of study.

In this microstudy, I explore the relationship between student workloads and course grades.

Specifically, the hypotheses being tested are:

H1H_1: Students who report being in paid employment will attain lower test scores than students who report not being employed.

H2H_2: Students who are enrolled in more courses attain lower test scores than students enrolled in fewer courses.

H3H_3: There will be a negative correlation between students' estimated total workload and test scores.

More or less — the hypothesis is that students who have a higher workload will get lower test scores.

Method​

The data collected for this study was gathered from a CS1 course designed for students who have no prior programming experience that teaches the basics of imperative programming using the Python programming language. The course has four computer-based tests spread throughout the semester run asynchronously during students' normal lab times. Data were collected over two semesters in 2024 — with the first semester acting as a pilot for the second. The questionnaire data in this study were gathered in Test 3 for both semesters.

The Pilot​

The pilot study was conducted during the summer semester (Jan – Feb) which is an intense 6-week semester (compared to the usual 15-week semester at the institution). In total, there were 84 students enrolled in the course.

Students fill in a paper attendance sheet at the start of each test that they must hand in before leaving the room. Beneath the name, ID, and seat number fields, I asked the teaching team to add the following questions:

A screenshot of text reading: Are you working in paid employment this semester (Yes/No)? \ If yes, how many hours per week do you work? \ 2. How many courses are you enrolled in this semester?. The no is circled and four courses are listed in extremely faint pink gel marker
An Answered Version of the Study Questions In the Faintest Ink Imaginable

The Main Study​

The main study was conducted during semester 1 (March – June) which is run over 15 weeks. In total, there were 676 students enrolled in the course.

The question given to students was not modified between the pilot and main study.

Results​

As in microstudy part 2, I am interested in the effect of employment and workload on test scores across all four tests. To analyse this, I took the average grades across all four tests for each student — ignoring missing test grades.

The Pilot​

For the pilot study run during the summer semester, 75 out of the 84 enrolled students sat the test, and of those, 67 students (89%) responded to the questionnaire. Only the data of those students who responded to the questionnaire will be used further.

The mean and median test scores were 66.5% and 65.6% respectively.

Employment​

Of the 67 students who responded to the questionnaire, 33 (49%) reported being in paid employment, and 34 (51%) reported not being in paid employment. The distribution of test scores is below:

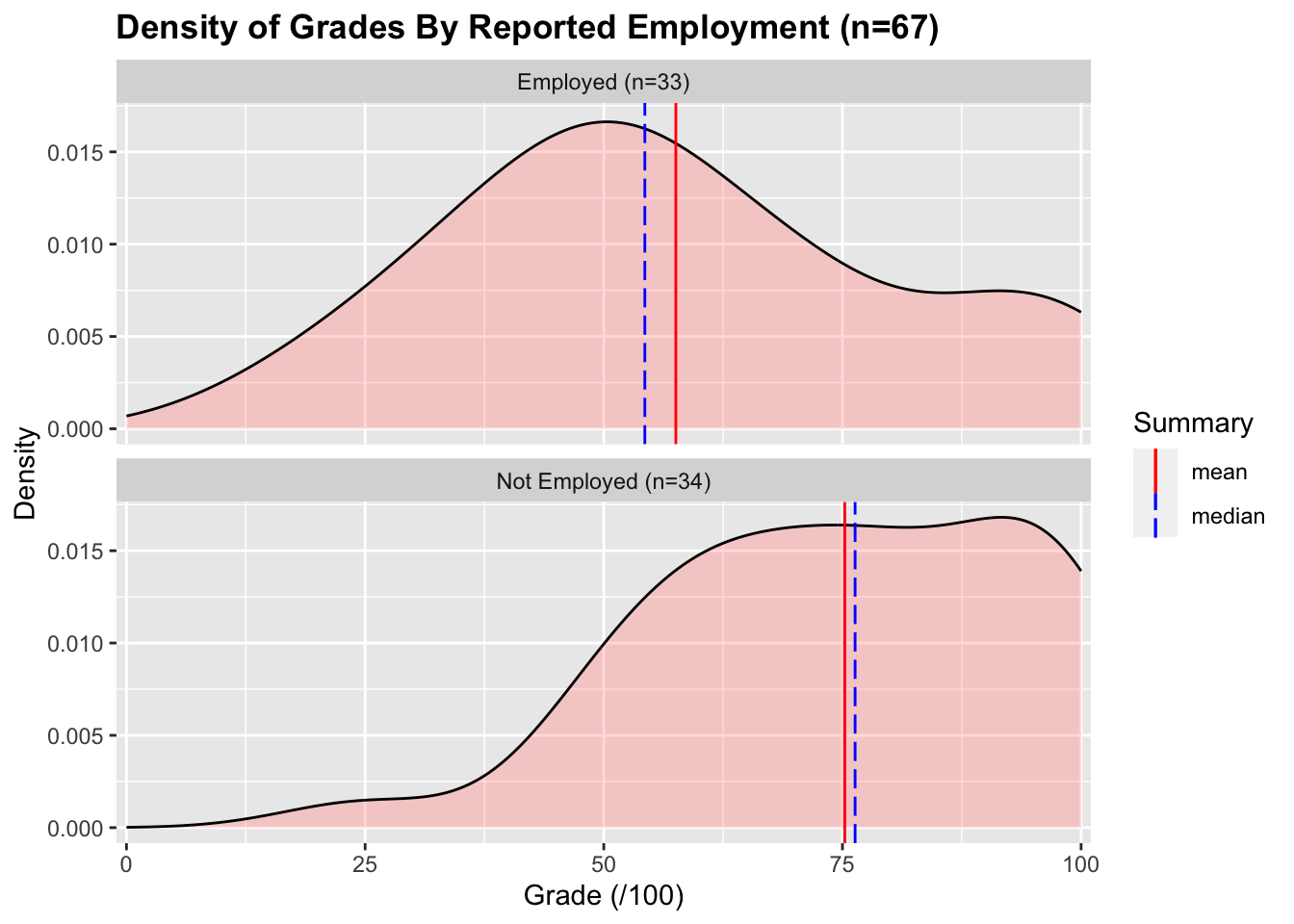
two stacked density plots of grades separated by reported employment. The employed group is not overly skewed and mostly centred with two lines showing the mean and median just above 50%. The not employed group is left skewed, with most of the data appearing in the top 50% of the grades. the stack positions of the charts clearly show the mean and median of the not employed group is a lot higher than the employed group.

The mean and median test scores for the employed group is 57.5% and 54.3% respectively. The mean and median for the not employed group is 75.2% and 76.3% respectively. The difference between these two groups is significant1 with a medium effect size2.

Hours Worked​

The students who reported being in paid employment reported a mean and median weekly workload of 18.8 hours and 15 hours respectively. The distribution of the hours worked per week is below:

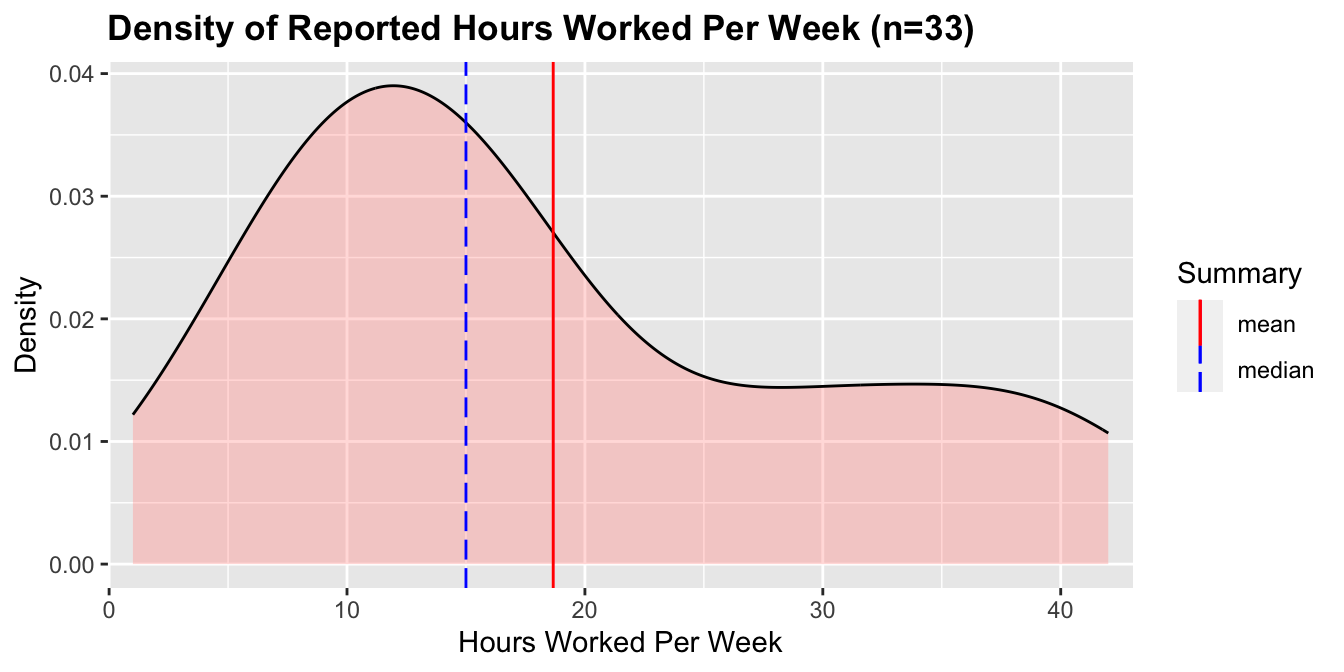
A density plot of hours worked per week. The data is right skewed with the mean just below 20 and the median around 15.

Note: for students who put ranges of hours (e.g. "5–7"), the average of the range was recorded.

There is no correlation between the hours worked per week and grades3

Coursework​

During summer school, it is common for students to only take one course. Students can enroll in a maximum of two courses during the summer semester. Of the 67 students who responded to the questionnaire, 39 (58%) were enrolled in one course and 28 (42%) were enrolled in two courses. The grade distributions are below:

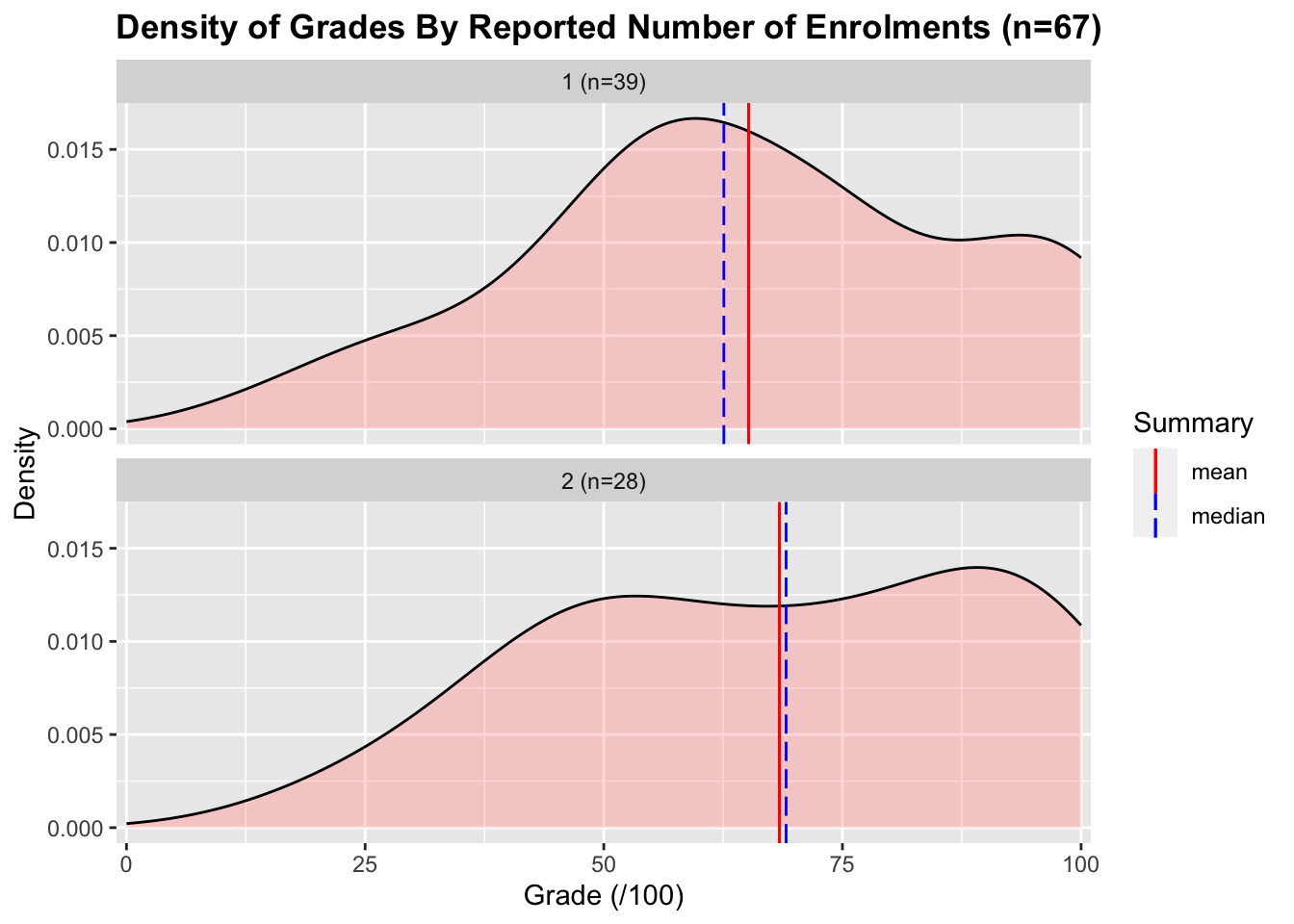
two stacked density plots of grades separated by reported number of enrolments. Both groups have similar means and medians, however, the two enrolment group seems slightly more left skewed than the one enrolment group.

The mean and median test scores for students taking one course were 65.1% and 62.6% respectively. The mean and median test scores for students taking two courses was 68.4% and 69.1% respectively. There is no significant decrease in grades between the one- and two-course groups4. In fact, the grades for the two-course group appear slightly higher than for the one-course group.

Estimated Workload​

The breakdown of employment and course enrolments is below:

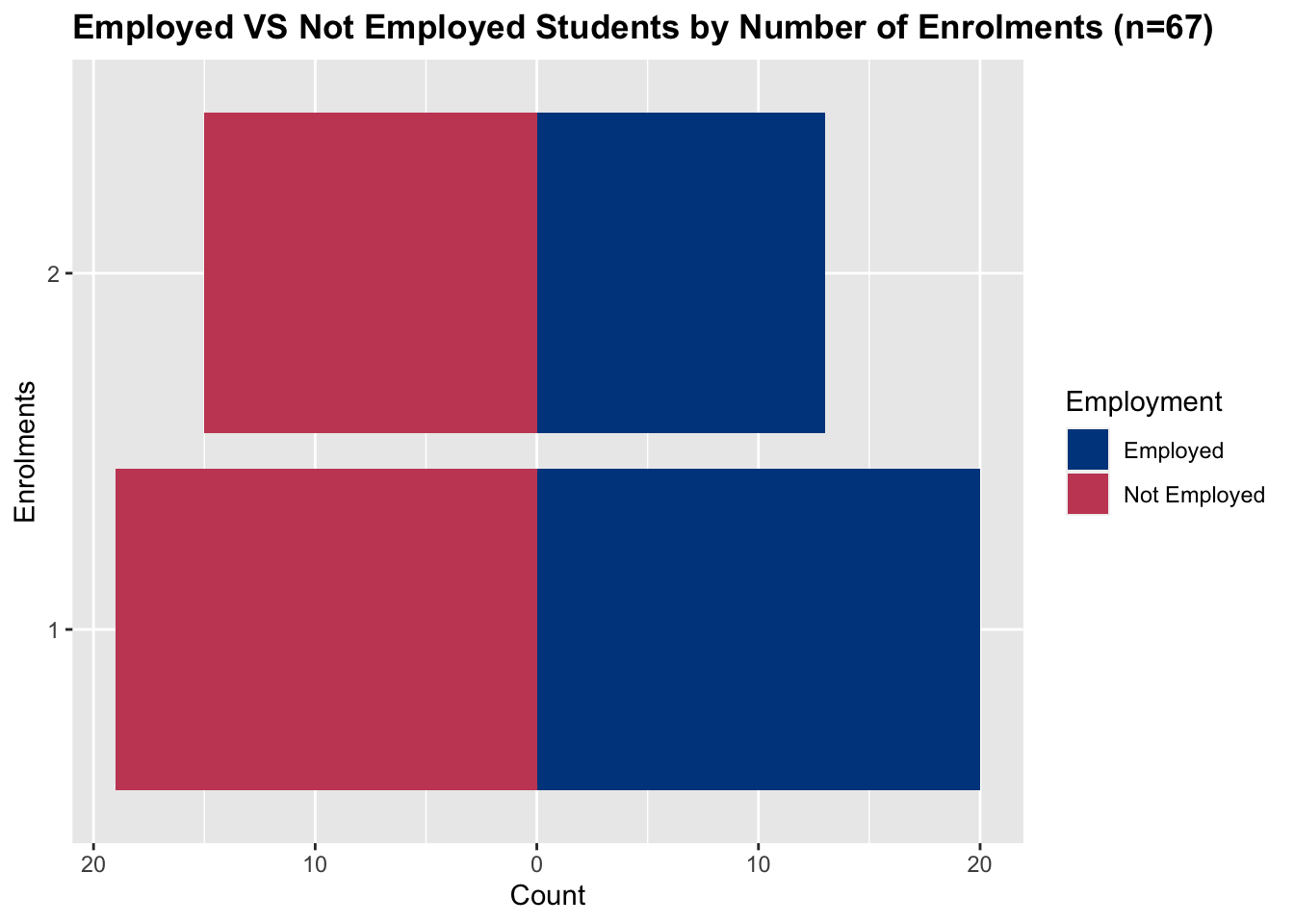
A violin plot of employment VS enrolments — the plot shows most students are enrolled in one course with approximately even proportions of students being employed and not employed. Fewer students are enrolled in two courses with a slightly higher proportion of students in this group being not employed

I have looked at the employment and enrolments of students individually; however, to combine these values, I estimate the weekly number of hours of work for each student. During summer school, students are expected to spend 20 hours studying for each course (this includes the time they spend in lectures and labs). An overall estimate is then calculated for each student by summing this expected coursework workload with the reported hours worked per week (if the student reports working). The distribution of estimated workload is below:

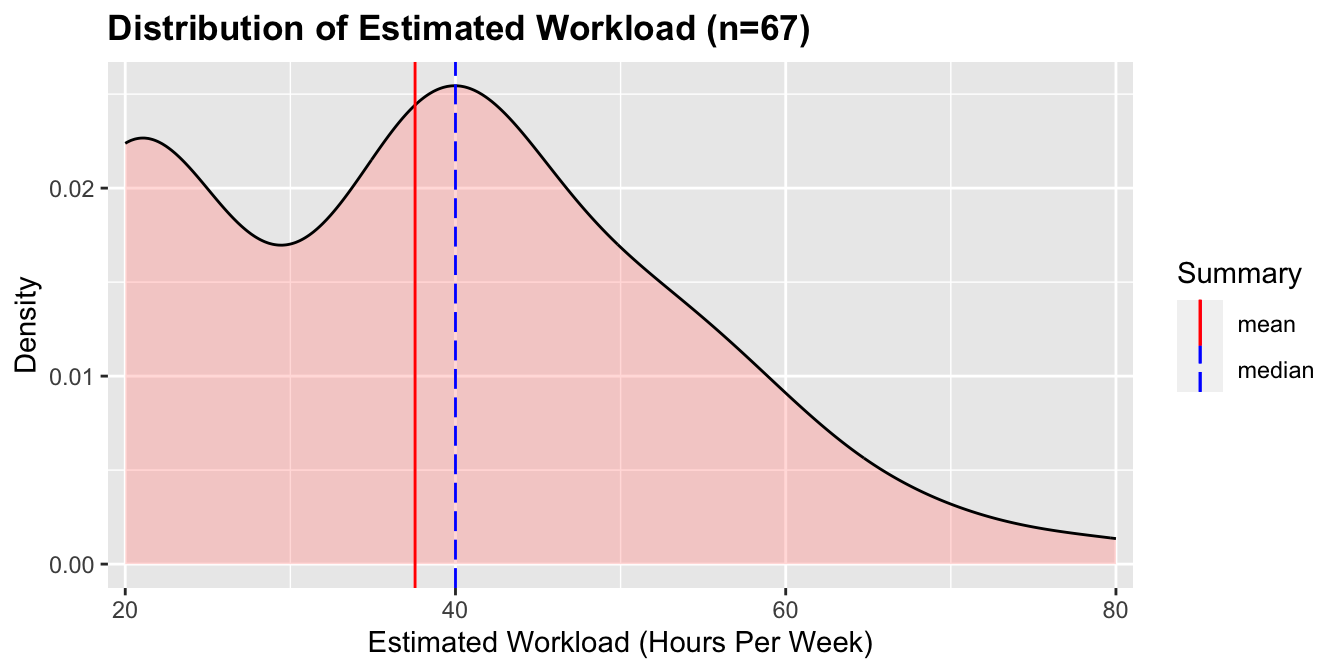
A density plot of the estimated weekly workload in hours. There are two peaks in the data, one at 40 hours and one at 20 hours. The data is left skewed

Students had a mean and median estimated workload of 37.6 and 40 hours per week respectively, with most students having an estimated workload of 40 hours.

The estimated workload is plotted against test scores below:

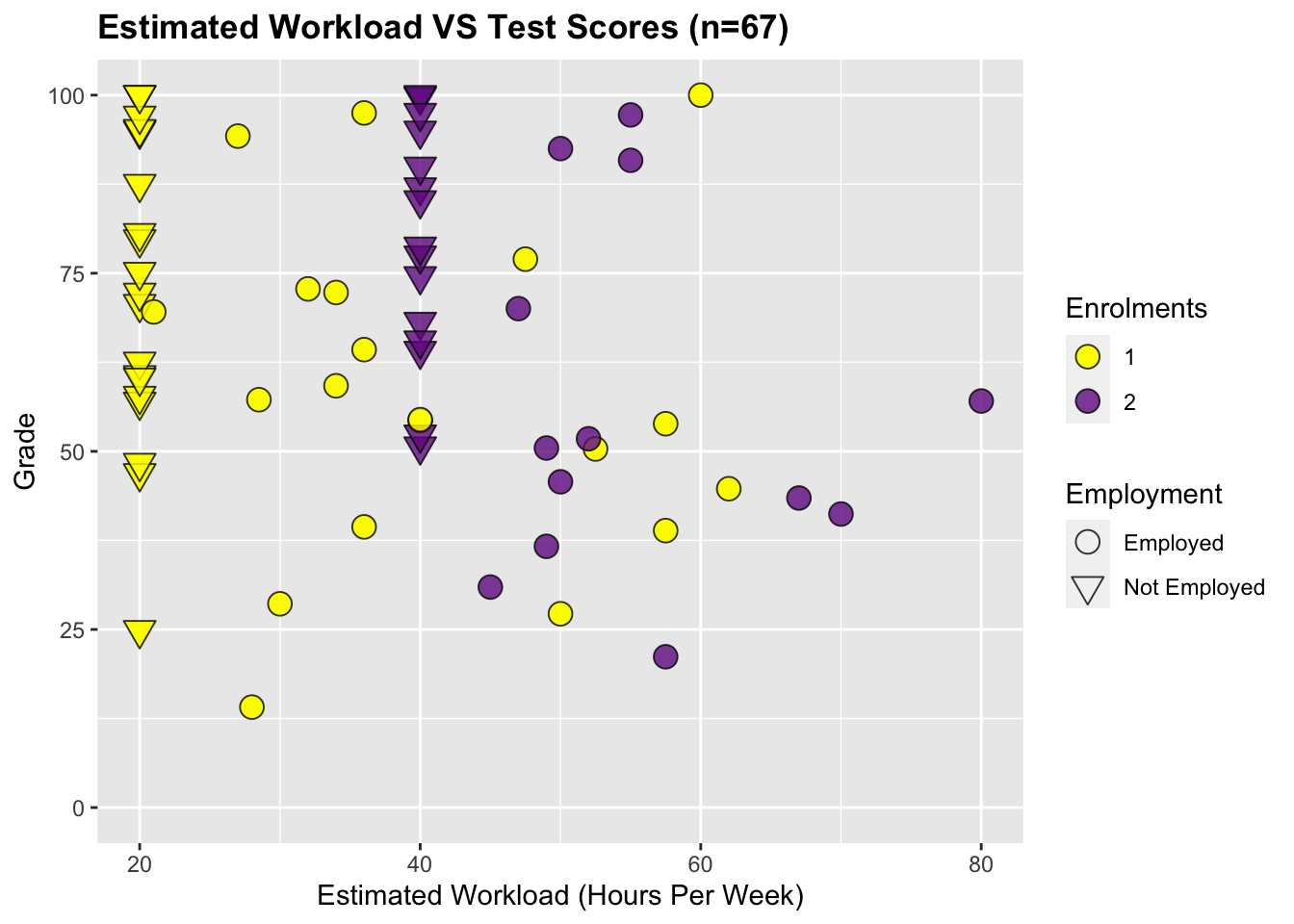
A scatter plot of estimated workload in hours per week vs grade. The points for the not employed students form two lines at the 20 and 40 hour mark for students doing one and two courses respectively. The points for the employed students do not show any obvious trend. Overall the graph does not show any trends except employed students seeming to have slightly lower grades.

There is a very weak negative correlation between the estimated workload per week and test scores5.

The Main Study​

For the main study run during semester 1, 591 of the 676 enrolled students sat the test, and of those 552 students (93%) responded to the questionnaire.

The mean and median test scores were 63.8% and 67.5% respectively.

Employment​

Of the 552 students who responded to the questionnaire, 205 (37%) reported being in paid employment, and 347 (63%) reported not being in paid employment. The distribution of test scores for the two groups is below:

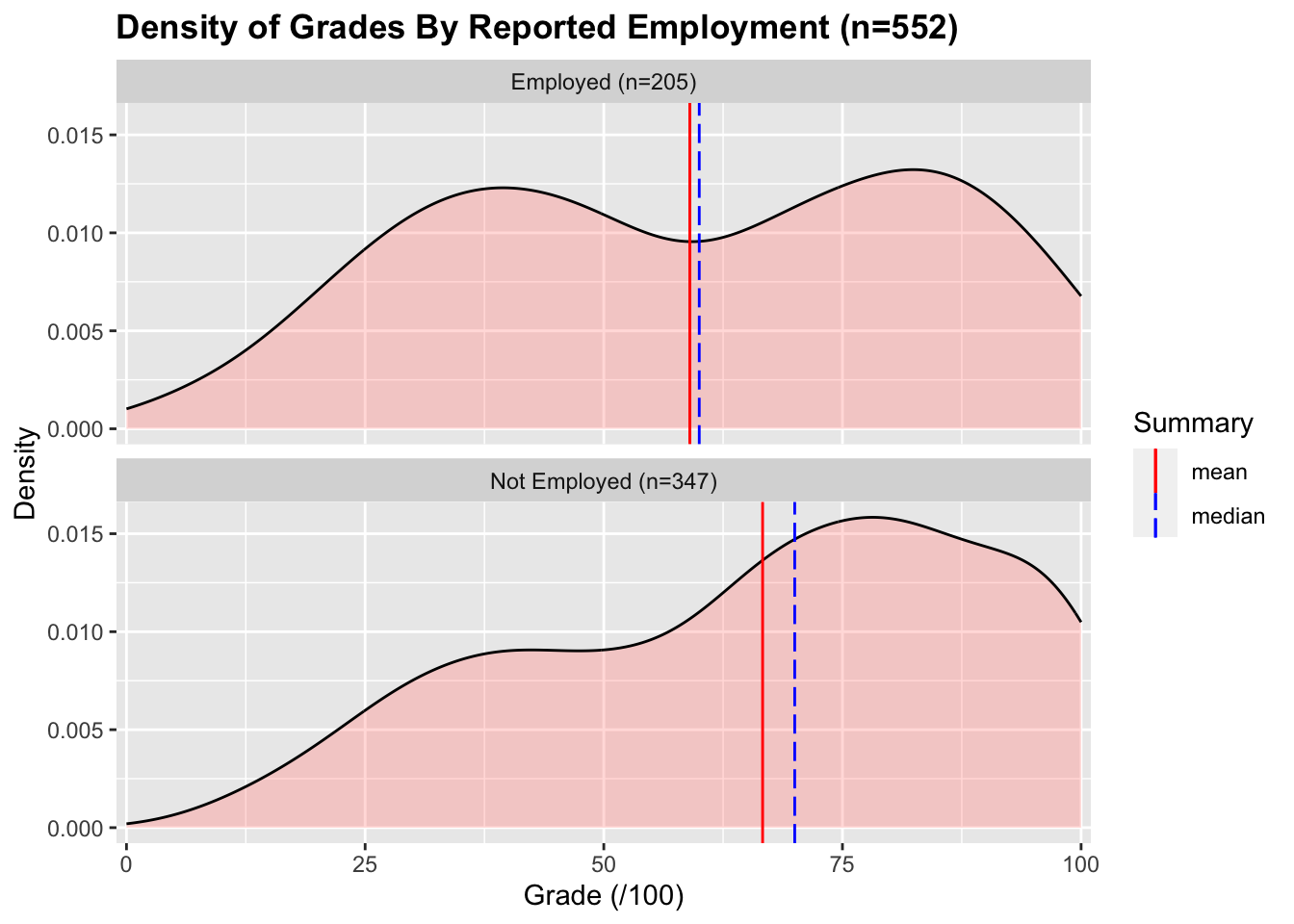
two stacked density plots of grades separated by reported employment. Both groups appear vaguely bimodal and are spread over most of the grade range and are both slightly left skewed. The stacked position of the charts shows the mean and median for the employed group is lower than the not employed group but there is still a lot of overlap between the two groups.

The mean and median test scores for the employed group are 59.0% and 60.0% respectively. The mean and median test scores for the not employed group are 66.6% and 70.0% respectively. The grades for the employed group are significantly lower than the grades for the not employed group6 with a small effect size7.

Hours Worked​

The students who reported being in paid employment reported a mean and median weekly workload of 12.9 hours and 11 hours respectively. The distribution of the hours worked per week is below:

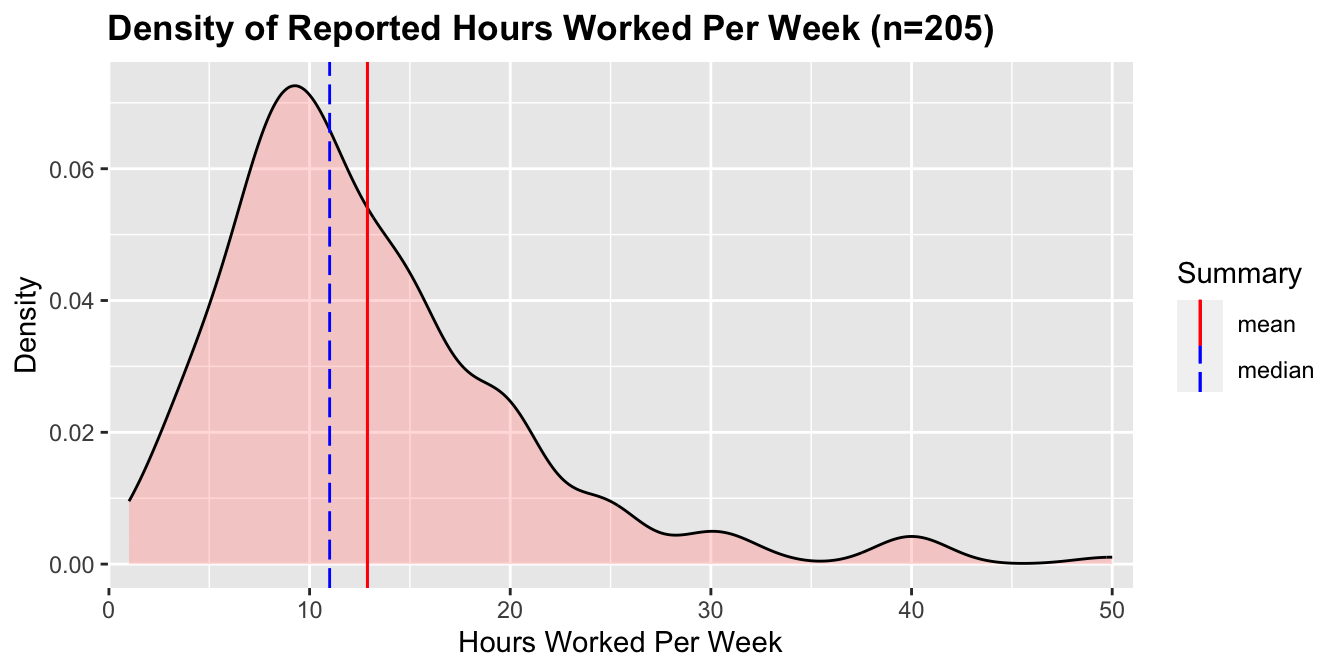
A density plot of hours worked per week. The data is right skewed with the mean and median just above 10

There is no correlation between the hours worked and grades8

Coursework​

During regular semesters, it is common for students to take four courses. Students can enrol in a maximum of five courses. The breakdown of enrolments and average test scores is below:

Summary of Number of Enrolments and Average Test Grades
#Courses n n% Mean (%) Median (%)
1 8 1.5 77.68 80.93
2 7 1.3 64.28 70.00
3 33 6.0 62.77 67.50
4 462 83.7 63.23 66.97
5 42 7.6 68.17 78.41

The grade distributions of these groups are below:

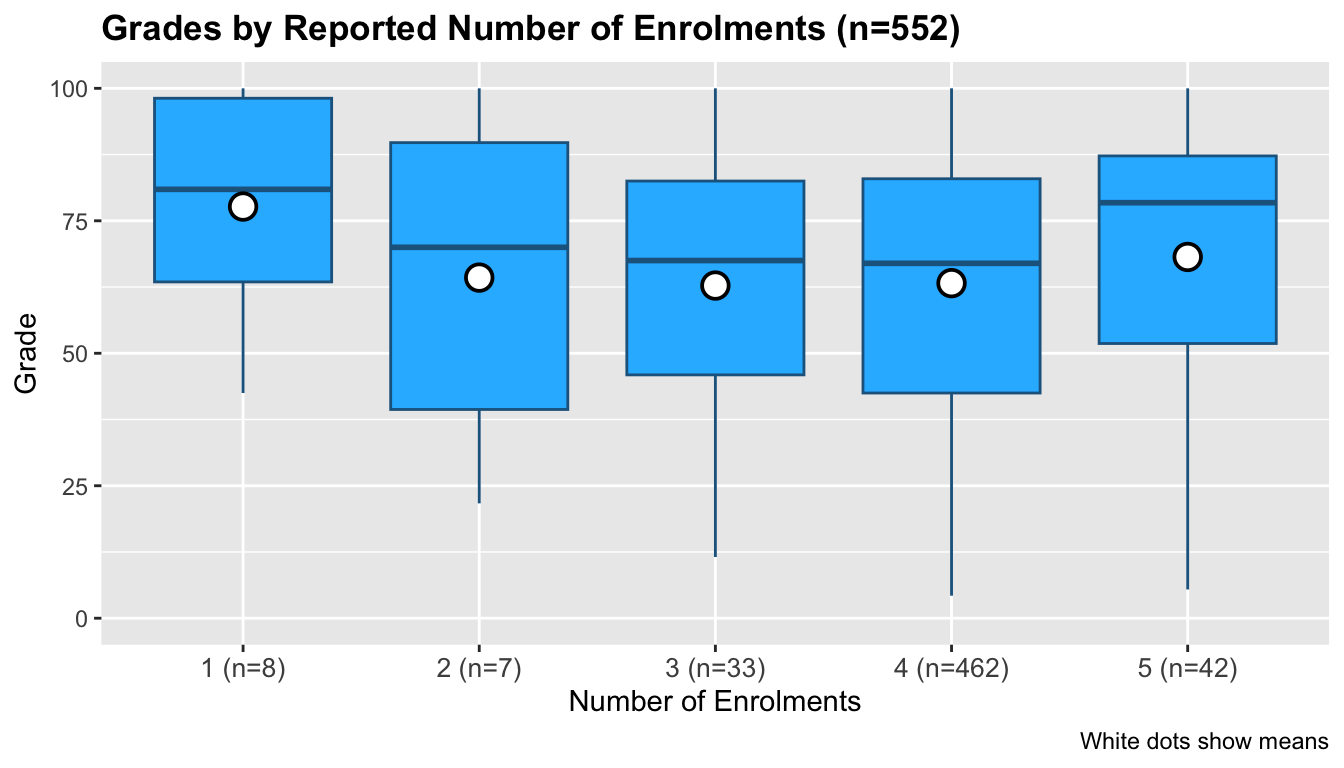
Several boxplots of the number of enrolled courses against grades. All box plots show left-skewed data. The box plots for 2 to 4 courses are all similar with medians around 70 and means around 65. The 1 and 5 course boxplots are slightly higher than the others.

A Spearman's rank correlation test shows no correlation between the number of enrolments and grades9.

Estimated Workload​

The breakdown of enrolments and employment is below:

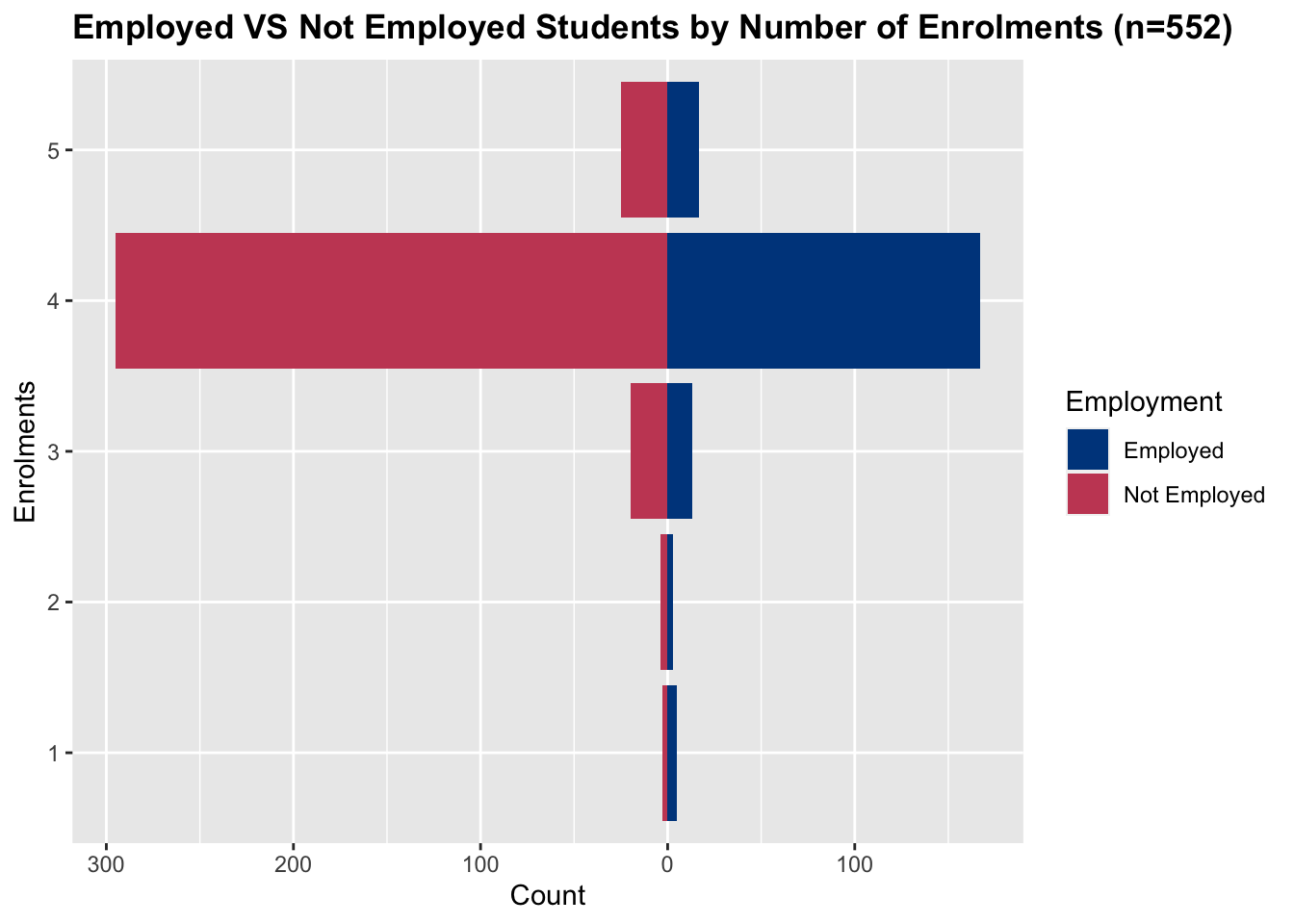
A violin plot of employment VS enrolments — the plot shows a large majority of students are enrolled in four courses. Across all groups, there appear to be more students who are not employed compared to the students who are employed.

As in the pilot, an estimate of student workload in hours per week is calculated. During normal semesters, students are expected to spend 10 hours studying for each course (this includes the time they spend in lectures and labs). An overall estimate is then calculated for each student by summing this expected coursework workload with the reported hours worked per week (if the student reports working). The distribution of estimated workload is below:

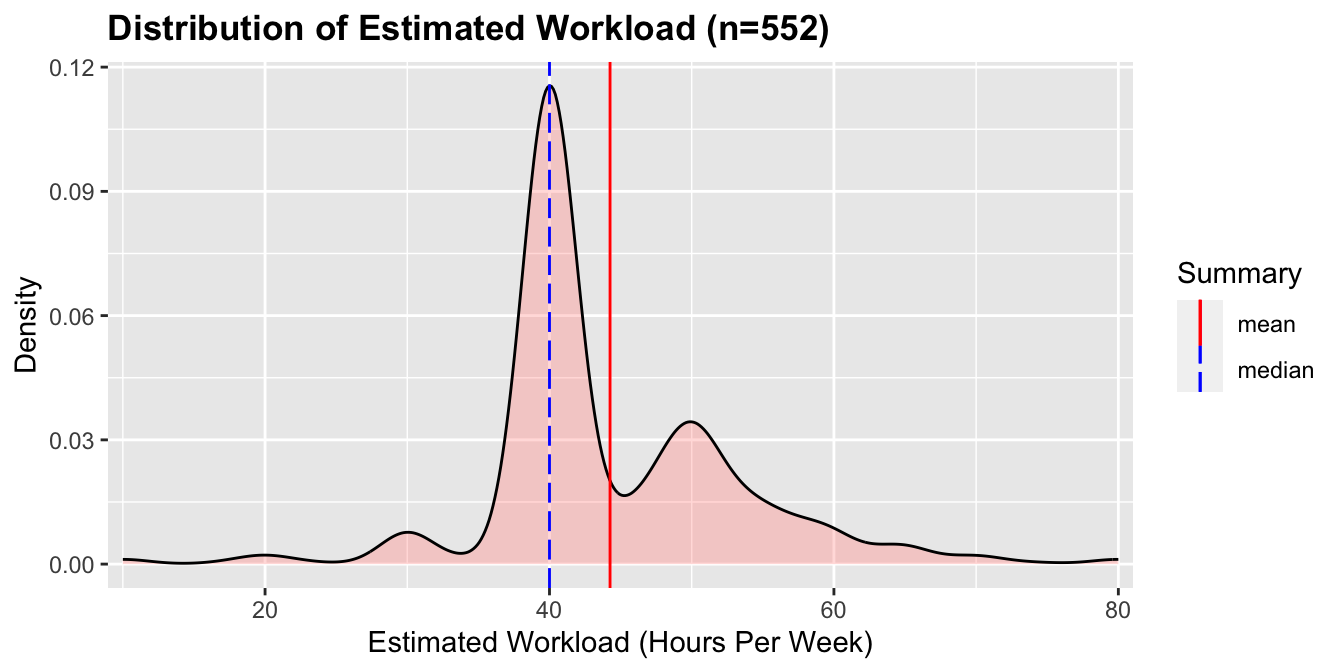
A density plot of the estimated weekly workload in hours. There is a large narrow spike at 40 hours per week. The plot is right skewed.

Students had a mean and median estimated workload of 44.3 and 40 hours per week respectively, with most students having an estimated workload of 40 hours.

The estimated workload is plotted against test scores below:

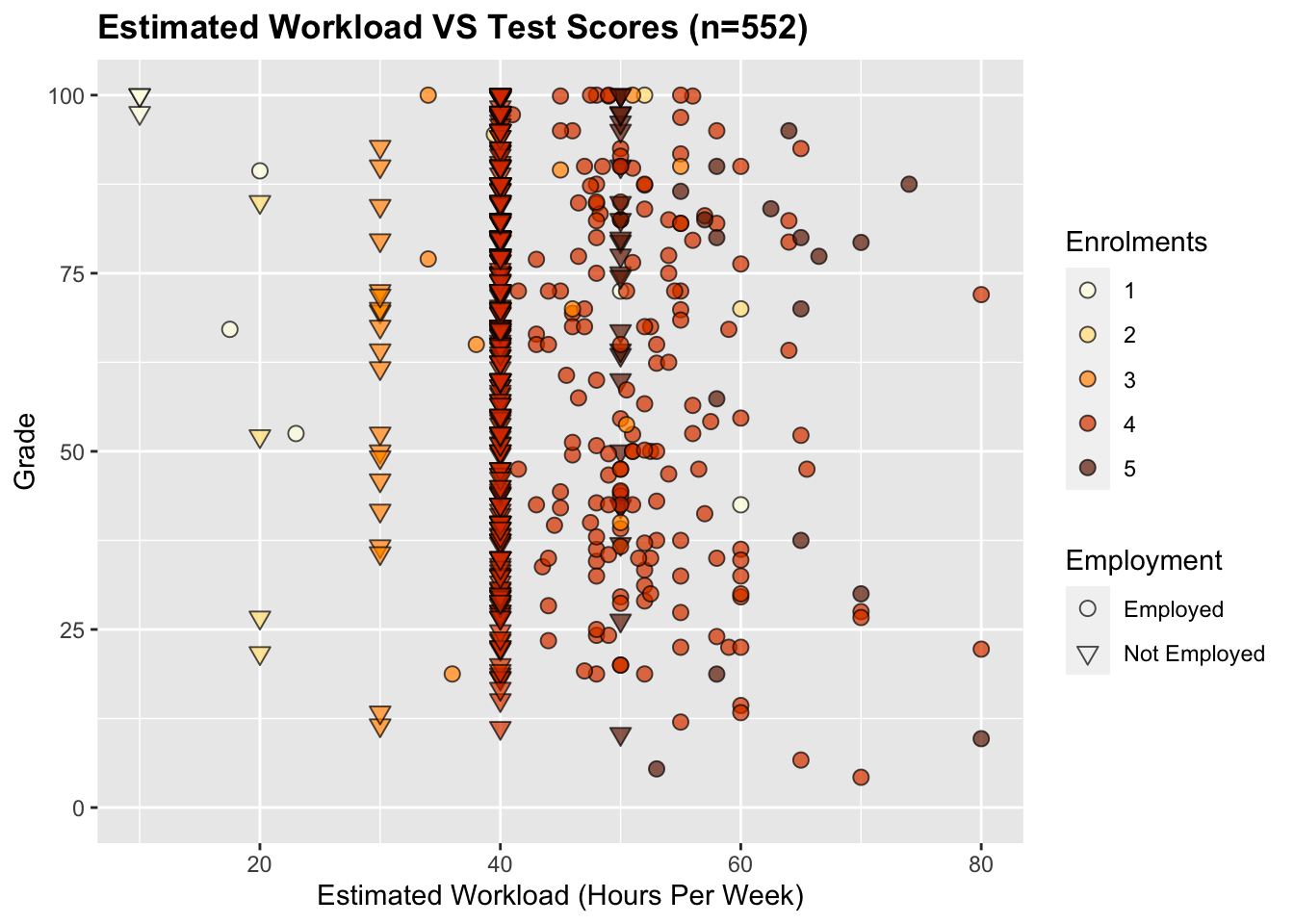
A scatter plot showing the estimated hours worked per week VS grades. Visually it seems as if there is a very slight negative trend — however, values are spread over most of the grade axis. Nodes are distinguished by number of enrolments and employment — but there is no obvious trend emerging from this data.

There is a very weak negative correlation between the estimated workload per week and test scores10.

Discussion​

Who knew you could fit so many density plots on to one little blog post! So far, the messiest microstudy.

There seems to be no correlation between the number of hours worked per week and grades, number of enrolled courses and grades, and not even the combination of the two — the estimated workload and grades. Despite this, there is a consistent drop in grades between the not employed students and the employed students across both semesters — but this effect is small.

From this we can tentatively accept H1H_1 and outright reject H2H_2 and H3H_3 — there doesn't seem to be any significant correlation between the number of course enrolments and grades, nor the overall estimated workload and grades; however, being employed seems to slightly negatively impact grades regardless of the number of hours worked or course enrolments.

Limitations​

As with the other microstudies, an obvious limitation of this study is the fact that only two cohorts of students were asked three questions on a self-selected questionnaire at a single institution in New Zealand. These results may not generalize to other countries or institutions.

Conclusions​

There are many follow-up questions I wish I could ask: What is the age distribution of the students who are working? What is the nature of their work — office based, or manual labour? Is their place of work close to their homes or the university? Do they mostly work on the weekends, or during the week? If students are working, is it out of necessity or for a bit of extra walking around money? If they could enroll in fewer courses, would they? If they could stop work, would they?

Those last three questions are interesting in the context of a New Zealand university. In addition to a course fees loan, the New Zealand student loan scheme allows students to get an allowance or loan for living costs of up to $316 per week11. However, there is only one first-year student accommodation plan at this university that costs less than this per week — and it is for a twin-share room plan, which is not common in New Zealand. Some eligible students are able to get an additional $60pw as accommodation support12 — but this increased amount of $376 only covers one more first year accommodation plan — with the other accommodation plans costing between $490 and $510 per week11. Amazingly, the apartment that has these two cheapest accommodation plans only has a capacity for 38 students13 — meaning many students living in other student accommodation will be at least $100–130 out per week. Thankfully, these accommodation plans are catered meaning there are no additional food costs.

Doing some back-of-the-napkin math, to cover the additional $100–130 rent and maybe have a scant $50 left over per week for other expenses, students would need to work between 7 and 9 hours per week assuming a minimum wage14 at the lowest tax-bracket15. To reiterate, this is the bare minimum a student who receives living costs in addition to accommodation support would need to work to afford shelter and food in university accommodation.

One suggestion might be for students to enroll in fewer courses and pick up more part-time work on the side to cover this discrepancy. Unfortunately, while working does not affect living cost loan eligibility, studying part-time does16. To be considered full time, students must enrol in seven courses per year (one fewer than the usual eight courses full-time students enrol in)17. This could put some students in a bind — they need to work to afford living costs and so have less time and energy for study, but need to study full time to be eligible for a student loan.

Not to belabour the point — but there is an equity argument to be made here. This study has shown employment has a small but negative impact on test score performance. Many students in the main study are enrolled in four courses (full time) while being in paid employment — obviously, we do not know the circumstances behind this (i.e. whether this is out of necessity or just for extra money) but New Zealand already has a problem with high school students needing to work during study and it would be unsurprising if these issues were to continue at the tertiary level.

Footnotes​

  1. The grades for the employed/not employed groups are just above the p=0.05 threshold for normality: Employed (W=0.96, p=0.248), Not Employed (W=0.95, p=0.090). However, as, visually, the groups do not appear normal, a more conservative 1-tailed Mann-Whitney test was performed over a t-test yielding: (U=304, p<0.001) ↩

  2. A Cliff's delta effect size test gave a statistic of -0.458 with a 95% confidence interval of -0.668 to -0.180 ↩

  3. A Spearman's rank correlation gives: r(31) = -0.051, p = 0.777 ↩

  4. As before, there is not enough evidence to reject the normality hypothesis: One course (W=0.96, p=0.221), two courses (W=0.94, p=0.138). However, as, visually, the data appears to be non-normal, a more conservative 1-tailed Mann-Whitney test was performed over a t-test yielding: (W=577.5, p=0.658). A cliffs delta shows a negligible effect size: -0.058 with a 95% confidence interval of -0.333–0.226. ↩

  5. A Spearman's rank correlation gives: r(65) = -0.241, p = 0.050 ↩

  6. The grades for the employed/not employed groups are not normal: Employed (W=0.96, p<1e-5), Not Employed (W=0.95, p<1e-8). A 1-tailed Mann-Whitney test was performed: (U=29695, p<0.001) ↩

  7. A Cliff's delta effect size test gave a statistic of -0.165 with a 95% confidence interval of -0.262 to -0.064 ↩

  8. A Spearman's rank correlation gives: r(203) = -0.078, p = 0.264 ↩

  9. A Spearman's rank correlation gives: r(550) = -0.021, p = 0.622 ↩

  10. A Spearman's rank correlation gives: r(550) = -0.118, p = 0.006 ↩

  11. Retrieved July 2024: https://www.studylink.govt.nz/products/a-z-products/student-loan/living-costs.html ↩ ↩2

  12. Retrieved July 2024: https://www.studylink.govt.nz/products/rates/accommodation-benefit-rates.html ↩

  13. Retrieved July 2024: https://www.auckland.ac.nz/en/on-campus/accommodation/accommodation-options/self-catered-accommodation/grafton-student-flats.html ↩

  14. Retrieved July 2024: https://www.employment.govt.nz/pay-and-hours/pay-and-wages/minimum-wage/minimum-wage-rates-and-types ↩

  15. Retrieved July 2024: https://www.ird.govt.nz/income-tax/income-tax-for-individuals/tax-codes-and-tax-rates-for-individuals/tax-rates-for-individuals ↩

  16. Retrieved July 2024: https://www.studylink.govt.nz/starting-study/whats-available/studying-part-time.html ↩

  17. Retrieved July 2024: https://www.studylink.govt.nz/about-studylink/glossary/efts.html ↩