Skip to main content

Microstudies: Part 2

Does Experience Count?

· 11 min read
James Finnie-Ansley

The goal of this microstudy is to evaluate the impact of self-reported prior programming experience on test scores in a tertiary-level introductory programming course. And, of students who report having prior experience whether the self-reported type of programming experience (e.g. high school course, self-taught, etc.) has an impact on test score performance.

Specifically, the hypotheses being tested are:

H1H_1: The test scores attained by students who report having prior programming experience will be higher than the test scores of students who report having no prior programming experience.

H2H_2: Of the students who report having prior programming experience, the self-reported type of prior programming experience will have no impact on test scores.

In short, the hypotheses are that any prior programming experience will improve grades — but the specific nature of the prior experience does not matter.

Method​

The course in question is a CS1 course designed for students who have no prior programming experience that teaches the basics of imperative programming using the Python programming language. The course has four computer-based tests spread throughout the semester run asynchronously during students' normal lab times. Data were collected over two semesters in 2024 — with the first semester acting as a pilot for the second. The questionnaire data in this study were gathered in Test 2 for both semesters.

The Pilot​

The pilot study was conducted during the summer semester (Jan – Feb) which is an intense 6-week semester (compared to the usual 15-week semester at the institution). In total, there were 84 students enrolled in the course.

Students fill in a paper attendance sheet at the start of each test that they must hand in before leaving the room. Beneath the name, ID, and seat number fields, I asked the teaching team to add the following yes/no question and categorical "circle one" question:

A screenshot of text reading "Did you have any programming experience prior to enrolling in CompSci101? Yes/No. If yes, was this experience via: high school course/self-taught/online course/other?"
The Pilot Study Questions

The Main Study​

The main study was conducted during semester 1 (March – June) which is run over 15 weeks. In total, there were 676 students enrolled in the course.

A few lessons learned from the pilot study:

  1. It is not obvious to students that they need to circle one of the options
  2. No one reported doing an online course
  3. Several students who circled "other" in the pilot indicated they had done another university course that had introduced programming.

From these lessons, an updated set of questions was added to the semester 1 attendance sheet:

A screenshot of text reading "Did you have any programming experience before enrolling in CompSci101 (circle one)? Yes / No - If yes, was this experience via (circle one): high school course / self-taught / other university course / other"
The Main Study Questions

Results​

Unlike microstudy part 1, I am interested in the effect of prior experience across all four tests given throughout the semester. To analyse this, I averaged the test scores for each student across all four tests, ignoring cases where a student did not sit a test1.

The Pilot​

For the pilot study run during the summer semester, 76 out of the 84 enrolled students sat the test, and of those, 58 students (76%) responded to the questionnaire. Only the data of those students who responded to the questionnaire will be used further.

The mean test scores across all four tests were 65.2% with a median of 64.9%.

Of the students who answered the questionnaire, 29 students reported having no prior programming experience, and 29 reported having some prior experience with programming. The grade distributions for each group are shown below:

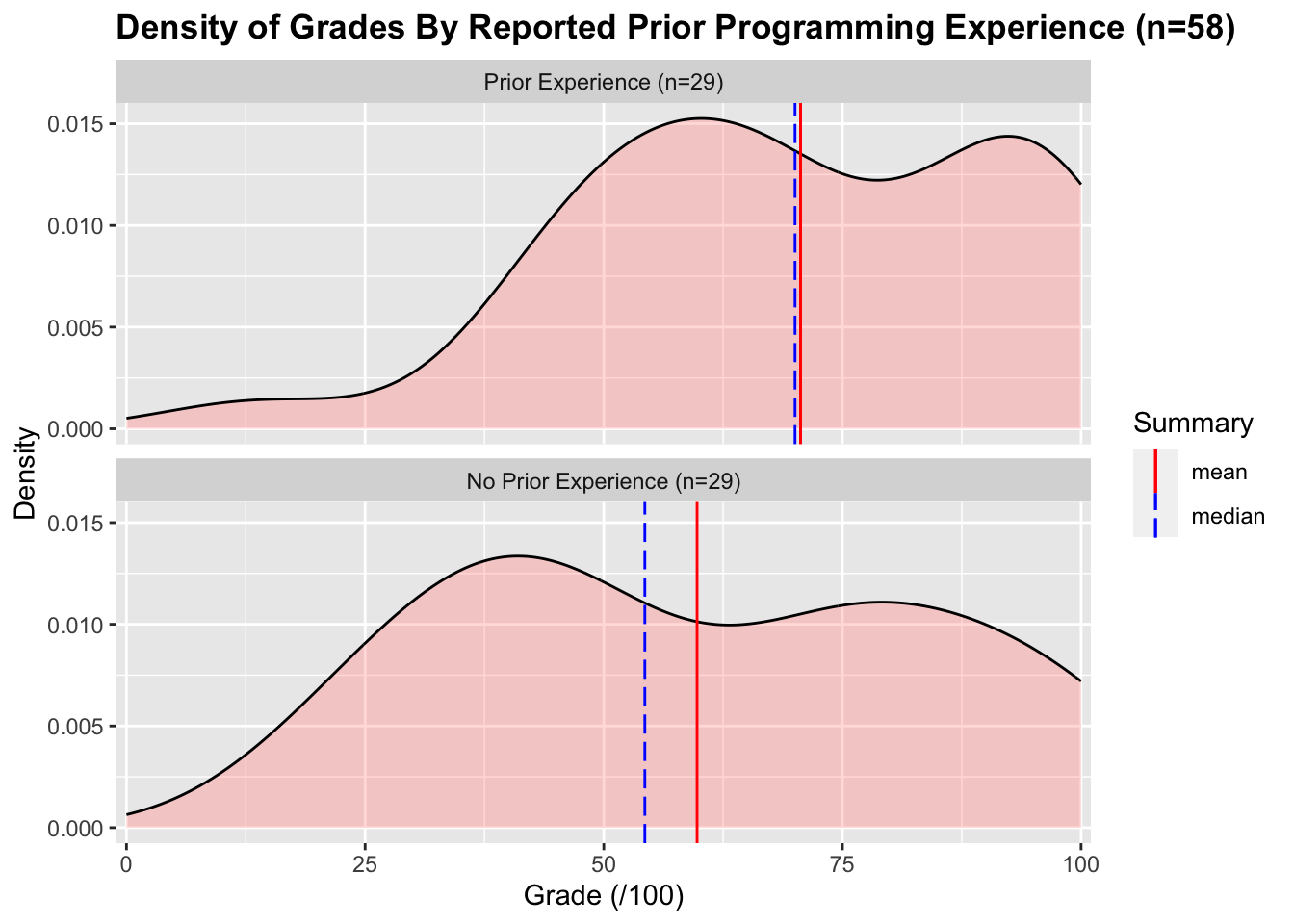
two stacked density plots of grades separated by reported prior experience. Both plots are vaguely bimodal, have quite a lot of spread, and are not overly skewed. Both plots have lines showing their means and medians. The prior-experience density plot has a mean and median around 70%. The no prior experience plot has a mean around 60% and a median around 55%. The stacked position of the charts clearly shows the mean and median for the prior experience group appears to be much greater than for the no-prior experience group. Despite this there is still quite a lot of overlap between the two groups

The mean and median grades for the prior experience group are 70.6% and 70.0% respectively. The mean and median grades for the no prior experience group are 59.8% and 54.3% respectively. The difference between these two groups is significant2 with a small effect size3.

Of the students who reported having prior experience, 9 reported the experience being primarily via high school, 10 reported being self-taught, and 10 listed "other". The ranges of the grades students in these groups attained are below:

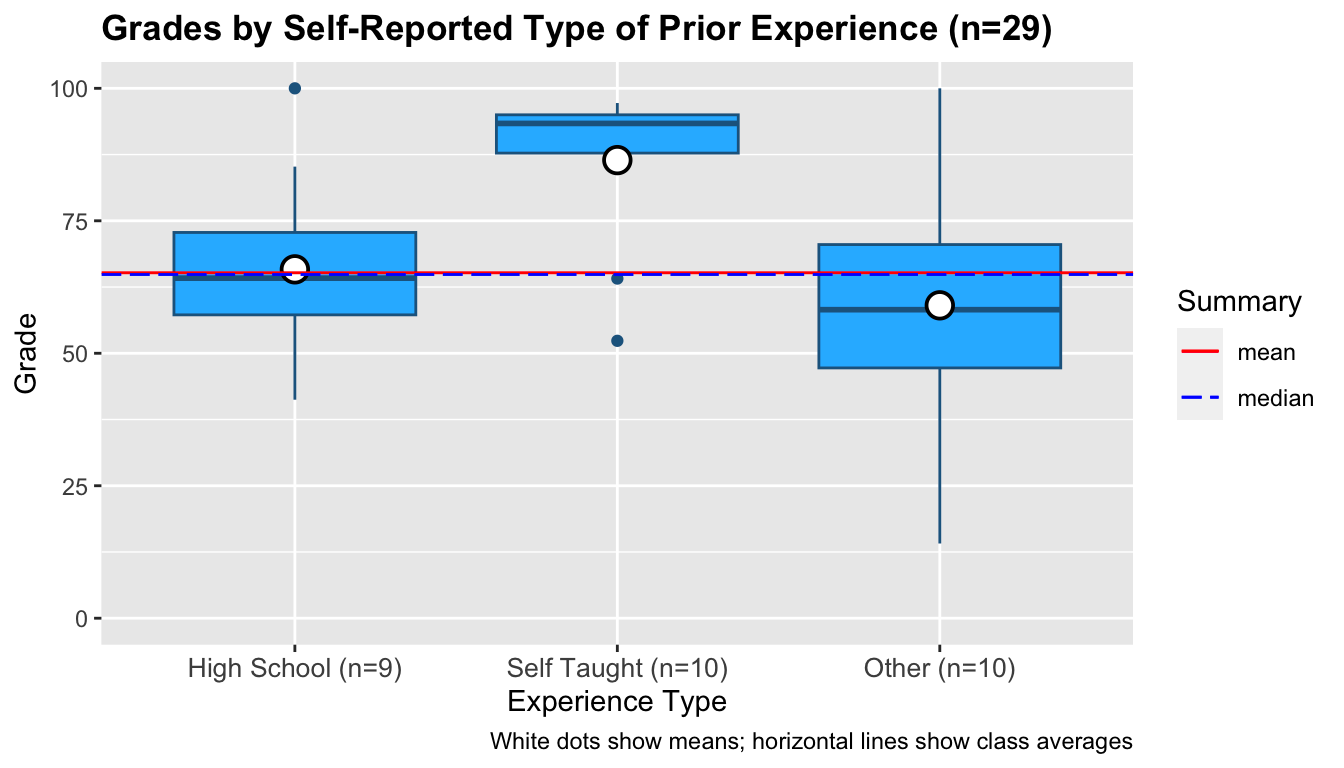
A box and whisker plot showing the three experience types: High school, self taught, and other against their respective grades. The self taught box is significantly higher than the other two — around the 90% range with almost no overlap with the high school or other box and whiskers. The high school and other plots are both spread around the class mean of 60% with their medians slightly lower than the class average. The other group is spread over a large range. The three plots do not seem particularly skewed.

Visually, the self-taught group appears well above the class average. A Kruskal-Wallis test indicates the means of these groups are different4 with a post-hoc analysis weakly indicating the self-taught mean is different from the other two groups5; however, the post-hoc analysis does not show significant results. This is likely due to the small sample sizes within each group.

The Main Study​

For the main study run during semester 1, 635 of the 676 enrolled students sat the test, and of those 526 students (83%) responded to the questionnaire.

The mean test scores across all four tests were 61.8% with a median of 66.6%.

Of the students who answered the questionnaire, 320 students reported having no prior programming experience, and 206 reported having some prior programming experience. The distribution of grades for each group is below:

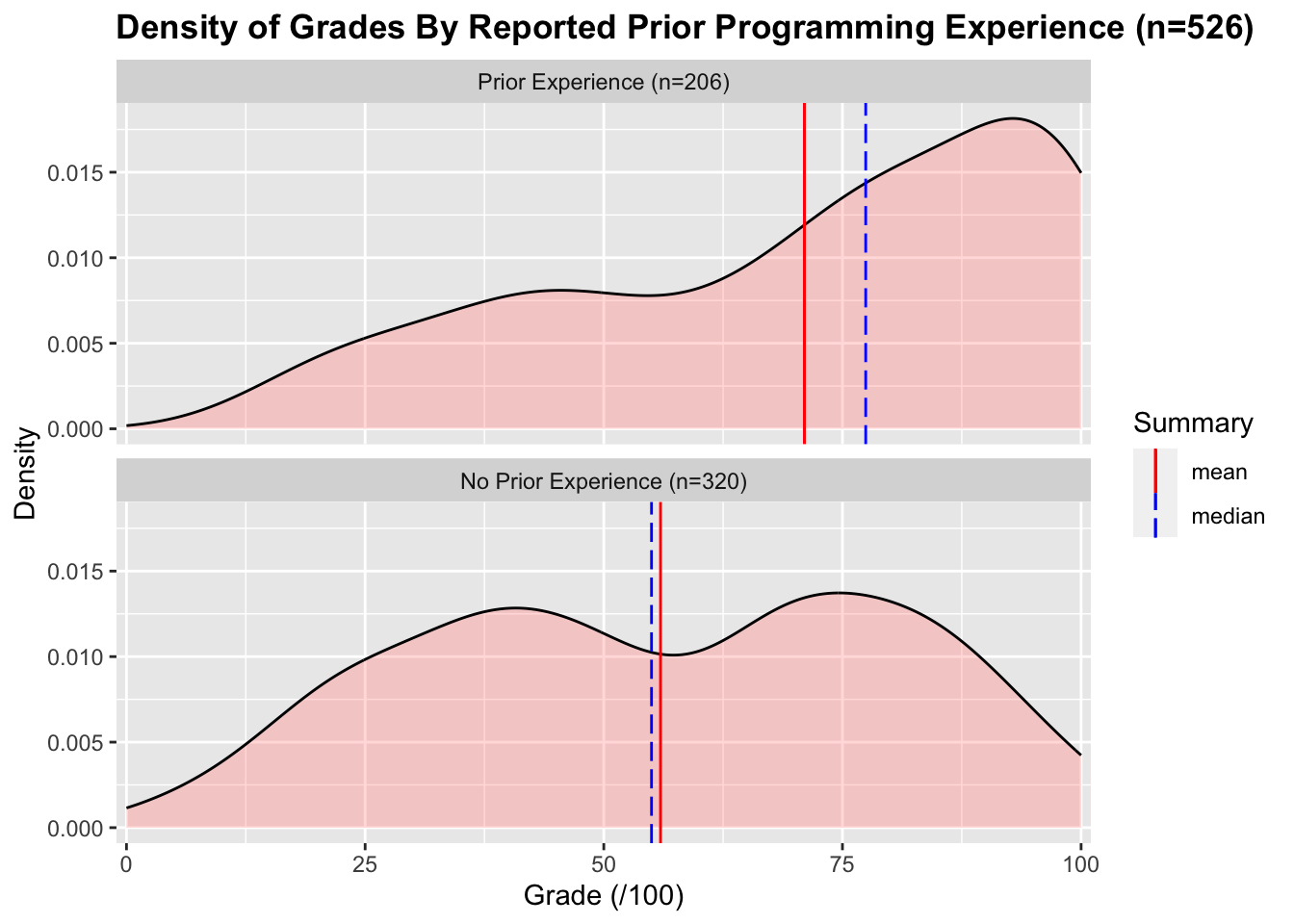
two stacked density plots of grades separated by reported prior experience. The prior experience plot is skewed left and srpead over the whole grade range. The no prior experience plot appears bimodal, is not overly skewed, and is spread over most of the grade distribution. Both plots have lines showing their means and medians. The prior-experience density plot has a mean around 70% and median around 80%. The no prior experience plot has a mean and median around 60%. The stacked position of the charts clearly shows the mean and median for the prior experience group appears to be much greater than for the no-prior experience group. There is still some overlap between the two groups but less than in the pilot study

The mean and median grades for the prior experience group are 71.0% and 77.4% respectively. The mean and median grades for the no prior experience group are 55.9% and 55.0% respectively. The difference between these two groups is significant6 with a medium effect size7.

Of the students who reported having prior experience, 130 reported their experience being primarily via high school, 8 reported "other", 22 reported another university course, and 46 reported being self-taught. The ranges of the grades students in these groups attained are below:

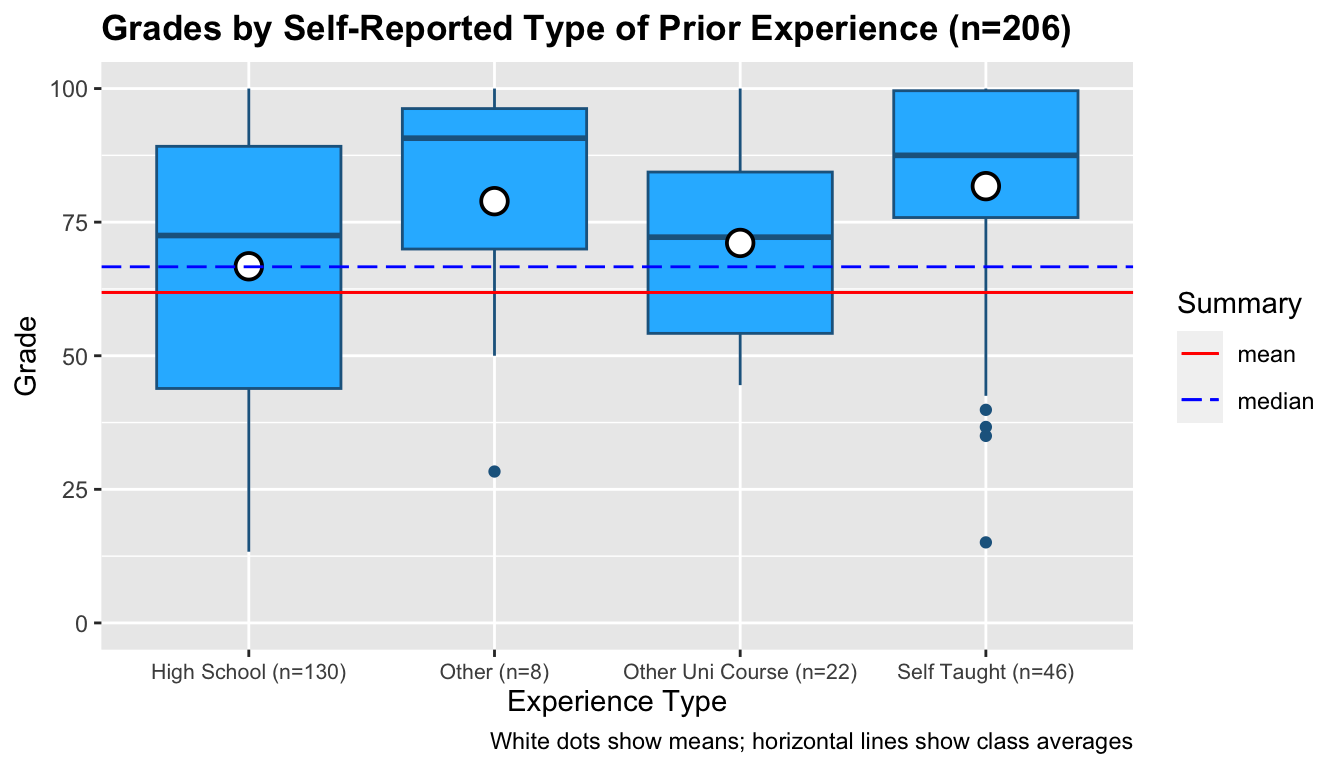
A box and whisker plot showing the four experience types: High school, other, other uni course, and self taught against their respective grades. The self taught and other boxes are significantly higher than the other two — around the 70 to 100% range. The high school box is spread over almost the entire grade range with its median only slightly above the class median. The other uni course box is spread around the class median with its slightly above the class average. The four plots do not seem particularly skewed.

Visually, the self-taught and other groups appear well above the class average. A Kruskal-Wallis test indicates the means of these groups are different8 with a post-hoc analysis showing a significant difference between self-taught grades and high school grades9.

Discussion​

From the results, there is enough evidence to accept H1H_1 — students who report having prior programming experience attain higher test-scores in an introductory programming course than students who report not having prior programming experience.

Interestingly, the type of prior programming experience does seem to have an impact — going against H2H_2. Specifically, students who report being self-taught attain significantly higher test scores than students who report having other types of programming experience.

Interestingly, high school programming experience does not seem to have any significant impact on students' test scores. Anecdotally, many teaching staff at this institution feel NCEA Level 3 digital technology programmes (what students are likely referring to when they list "High School" programming experience at this university) do not adequately prepare students for tertiary-level programming. This anecdotal evidence seems to be mostly validated by the results of this study.

Limitations​

One obvious limitation of this study is that I only asked two cohorts of students at a single institution two simple categorical ("circle one") questions in a self-selected questionnaire.

Conclusions​

So, does experience count? Well, if that experience is being a self-taught programmer in a tertiary-level introductory programming course, then, yes. The fact that self-taught students perform significantly better than other students with prior experience is interesting. A possible explanation for this is that self-taught students are motivated enough to learn programming in their own time and that motivation, not mere exposure to programming, leads to higher grades. A possible follow-up study could try to gauge this by asking students at different stages of programming-focused degrees whether they work on programming projects outside their normal university coursework.

The results of this study have been consistent over two semesters — self-reported prior programming experience does correlate with higher test scores; and, interestingly, the type of prior experience students reported having had an impact on test scores as well.

This study does not attempt to validate "how much" prior experience students have — nor does it attempt to get any kind of objective metrics beyond the avenues students think they primarily attained their prior experience. This is in contrast with other studies that attempt to examine the programming constructs students are familiar with, ask questions about "program size" or getting students to compare themselves with experts, or even the number of git commits students made prior to enrolling in a course. Despite this study's supposed limitations, it was able to show a marked difference between students with and without prior programming experience. It could be that much simpler measures can be taken to quickly gauge the ability of different students in introductory programming courses.

Footnotes​

  1. That is, taking the average of the test scores for the tests the students did sit. The rationale for this is that at our institution, if a student cannot sit a test due to some unavoidable reason (like sickness), they are granted an aegrotat score which is usually calculated as the average of their other test scores. From the data collected, it is not known why a student did not sit a test or whether they were granted an aegrotat. ↩

  2. The grades for the prior/no prior groups are just above the p=0.05 threshold for normality: Prior experience (W=0.94, p=0.08), No prior (W=0.93, p=0.07). However, as, visually, the groups do not appear normal, a more conservative 1-tailed Mann-Whitney test was performed over a t-test yielding: (U=529, p=0.047) ↩

  3. A Cliff's delta effect size test gave a statistic of 0.258 with a 95% confidence interval of -0.052 to 0.523 ↩

  4. The groups are not all normal: High school (W=0.961, p=0.809), Self taught (W=0.708, p=0.001), other (W=0.969, p=0.878). A Kruskal-Wallis test showed that there was a significant difference of the means H(2, n=29) = 7.106, p = 0.029 ↩

  5. A pairwise Wilcox test with holm correction shows no difference between the other group and high school (p=0.567) but a weak difference between self-taught and high school (p=0.091) and self-taught and other (p=0.052). ↩

  6. The grades for the prior/no prior groups are not normal: Prior experience (W=0.91, p<1e-9), No Prior (W=0.97, p<1e-5). A 1-tailed Mann-Whitney test was performed: (U=44414, p<1e-11) ↩

  7. A Cliff's delta effect size test gave a statistic of 0.348 with a 95% confidence interval of 0.249 0.439 ↩

  8. The groups are not all normal: High School (W=0.924, p<1e-5), Other (W=0.809, p=0.035), Other Uni Course (W=0.939, p=0.185), Self Taught (W=0.809, p<3e-5) A Kruskal-Wallis test showed that there was a significant difference of the means H(3, n=206) = 16.304, p = 0.001 ↩

  9. A pairwise Wilcox test with holm correction shows no significant difference between any groups except High School and Other (p=0.001) and a slight difference between High School and Other Uni Course (p=0.064). ↩